Fundamental of Reinforcement Learning 공부 정리!!(5)

MDP의 value funtion 사이의 연관성을 나타내는 식. Bellman Equation.

Bellman Expectation Equation

앞서 보았듯이 value function은 크게 policy, action value function으로 나타난다.

일반적인 value function 부터 policy, action function을 Return의 정의에 따라서 풀어쓰고 discount ratio로 묶으면 bellman equation 이라고 부른다.  

이렇게 expectation으로 표현하는 것은 좀 이해하기 힘들수도 있으니 다른 방식으로 표현해보자.

현재 state 의 value function과 다음 state의 value function의 상관관계의 식을 구하려면 

state-action pair에 대해 관계를 나눠볼 필요가 있다.

state-action pair는 어떠한 state에서 어떤 action을 행한 상태 를 또다른 state로 생각하는 개념.

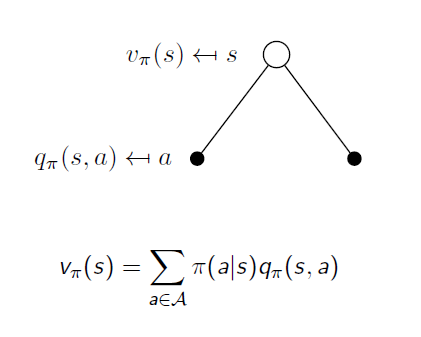
흰점은 state, 까만점은 state-action pair를 의미. 가지는 여러개가 될수 있음.

state에서 선택할수 있는 action의 수와 같음.

v와 q의 관계가 policy 로 위의 식으로 나타낼수 있음.

각 action을 할 확률과 action 의 결과인 expected return 을 곱한 것을 더하면 현재 state의 value function 이 된다.

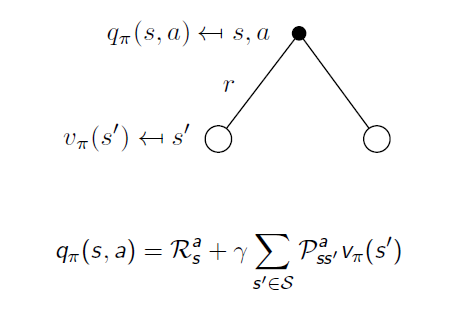
보상인 reward를 추가해 그린 그림이다. 

reward의 정의에 state와 action이 조건으로 들어가기 때문에 state - action pair 로 까만 점으로 표시한것이다.

action에서의 가지는 state transition probability matrix 를 나타낸다.

action value function은 직전 reward에 action을 취해 각 state로 갈 확률을 곱하고, 그 위치에서의 value function을(discount된) 더한 것으로 표현 할수있다.

두가지의 그림을 합치면

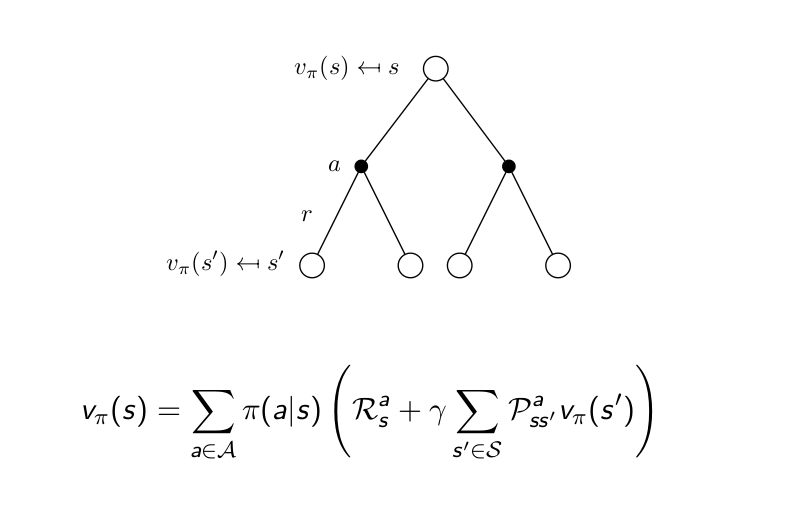
강화학습을 시작할때는 reward와 state transition probability는 미리 알수 없다. 학습을 통해서 얻는 것이기때문.

이 두가지를 다 알게된것이 MDP의 모델이 되는것.

따라서 reward function과 state transition probability를 모르고 학습하는 강화학습의 경우 bellman equation으로 구할수 없다.

같은 식을 action value function에 대해 적용하면 아래와 같다.

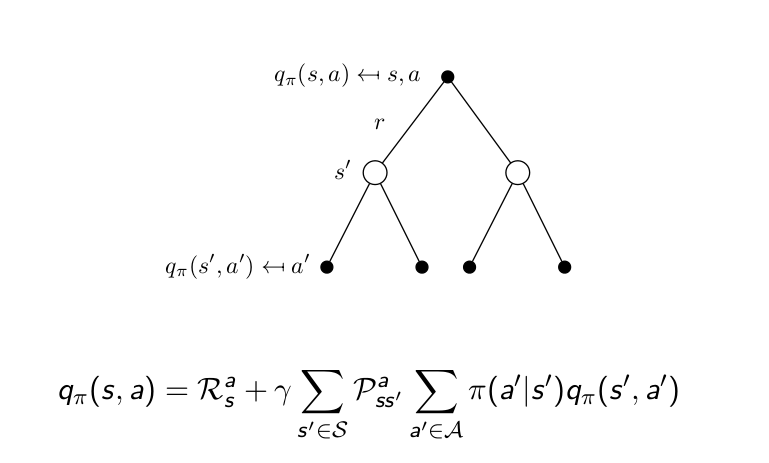
Bellman Optimality Equation

이전에 살펴본 bellman equation은 기대값의 형태로 표현한 것.

이전 식에서의 등호는 코딩에서의 대입에 가깝다.

그래서 backup이라는 개념이 등장한다.

그림에서 미래 state value function으로 현재 value function을 구한다는 것이 backup 이다.

자세한 것은 다음에.

optimal value function부터..